Epidemics:ferguson2008
| Virtual society | Virus spread | Literature | Version |
|---|---|---|---|
| Polish virtual society epidemics model | |||
| Guinea pigs epidemics model | |||
| Virus genetic evolution epidemics model | |||
Model
An example of so called SIR (Susceptible, Infectious, Recovered) model[1].
Joint probability of observed (Y), unobserved variables (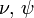 ), and parameters (
), and parameters (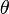 ) is given by:
) is given by:
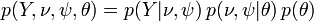 ,
,
where:
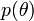 ,
,  prior level (prior distribution of the parameters of the model).
prior level (prior distribution of the parameters of the model).
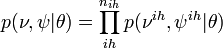 ,
,  transmission level
transmission level
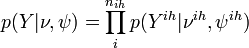 ,
,  observation level
observation level
Y - indicator function: 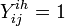 (for ith, (
(for ith, (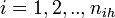 ) individual of ihth household (of size
) individual of ihth household (of size 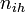 ) on jth day (
) on jth day (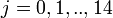 )), if clinical influenza was observed,
)), if clinical influenza was observed, 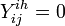 otherwise.
otherwise. 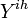 - all observations from household ihth, Y - observations from all households.
- all observations from household ihth, Y - observations from all households.
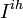 - group of individuals at ihth household with at least 1 day of clinical influenza,
- group of individuals at ihth household with at least 1 day of clinical influenza, 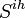 - remaining members of the ihth household.
- remaining members of the ihth household.
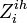 - the 1st day of clinical influenza of ith individual in ihth household
- the 1st day of clinical influenza of ith individual in ihth household
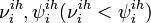 - unobserved variables corresponding to the start and the end of the infectious period for ith individual of ihth household
- unobserved variables corresponding to the start and the end of the infectious period for ith individual of ihth household
Transmission level
The instantaneous risk of infection for an individual at time t in household of size n:
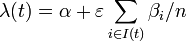 ,
,
where 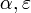 - instantaneous risk of infection from the community and within household, respectively.
- instantaneous risk of infection from the community and within household, respectively.
The duration of infectious period for ith infective 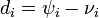 is taken from gamma distribution with mean
is taken from gamma distribution with mean 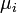 and standard deviation
and standard deviation 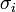
Observation level
Prior level
That is prior distribution of parameters, 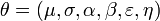
References
- ↑ CAUCHEMEZ S, Carrat F, Viboud C, Valleron A J, Boelle P Y, A Bayesian MCMC approach to study transmission of influenza: application to household longitudinal data, Stat. Med., 23, (2004), p3469