Epidemics
From RiversWiki
| Virtual society | Virus spread | Literature | Version |
|---|---|---|---|
| Polish virtual society epidemics model | |||
| Guinea pigs epidemics model | |||
| Virus genetic evolution epidemics model | |||
Contents
Pandemics history info on the Internet
Past Pandemic Timeline in Nature
H5N1 outbreaks in birds and other animals in Nature
Human cases of avian flu in Nature
Influenza report 2006 - on-line book
Important parameters
- Basic reproductive number,
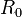 - the mean number of secondary cases a typical single infected case will cause in a population with no immunity to the disease in the absence of interventions to control the infection.
- the mean number of secondary cases a typical single infected case will cause in a population with no immunity to the disease in the absence of interventions to control the infection.
Review of epidemics models
Ferguson's, in France[1][2]
Quite large amount of data on epidemics in France from Sentinel and Centre National de Reference de la Grippe, region Sud, Laboratoire de Virology.
- workplaces not explicitly included
- transmission model: probability of the infection of the individual i,
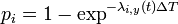 , where
, where 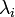 is the instantaneous infection risk of the individual i.
is the instantaneous infection risk of the individual i. - transmission rate in a household
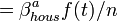 , where a - age (Adult(>=18) or Child), f(t) - relative infectiousness according to time t since infection, n - the size of the household.
, where a - age (Adult(>=18) or Child), f(t) - relative infectiousness according to time t since infection, n - the size of the household. - transmission rates for: within household infection (A,C), within school, within community (A->A,C->C,A<->C). Hence, the overall risk of infection includes: the household risk, the within school risk, the community risk
- time step = 6h
- annual variations of influenza infections modeled via: the strength of transmission during the year and the relative contribution of children to transmission during the year (included in
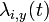 ), where y - year
), where y - year
Ferguson's, in UK and USA[3]
- households, schools, workplaces included in the model
- commuting data also included (the average distances traveled from hh to wp); the UK distance distribution more-less like power law, that of USA - surprisingly a bit different
- air travel data included
- time step = 6h
- transmission model: probability of the infection of the individual i,
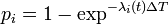 , where
, where 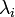 is the instantaneous infection risk of the individual i.
is the instantaneous infection risk of the individual i.
Ferguson's, in Thailand[4]
- households, schools, workplaces included in the model
- travel data - not enormous, but some, generalized into probabilities of commuting within district
- seasonality not included (available data suggested that climate changes do not influence the infectivity rate)
Ferguson's in UK[5]
Dunham's general model - MASON[6]
Germann's, in USA[7]
- no seasonal or environmental factors included, no virus evolution effects included
- basic geographic unit corresponds to census tract, it is a community of 2000 individuals: age, household size, and employment status distributions match US census data; agents divided into 5 age groups (0-4, 5-18, 9-29, 30-64, 64+ years) or community with no residents, only a workplace of about 100 individuals; in total, about 180000 communities are included; also travel data for the members of community included (in census tracts info);
- playgroups or daycare centers, schools, workplaces included; also contacts with people from neighborhood, occasional contacts in churches, supermarket, etc, included
- time step = 12h
- transmission model: probability of infection from a single contact,
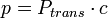 , where
, where  is the contact probability (dependent on the age of both contacting people),
is the contact probability (dependent on the age of both contacting people), 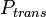 is the probability of transmission; antiviral treatment of the infectious contact person or the vaccination of the given individual diminish the
is the probability of transmission; antiviral treatment of the infectious contact person or the vaccination of the given individual diminish the 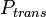 ;
;
Total probability of the susceptible person to get infected, 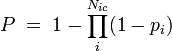 , where the product goes over all
, where the product goes over all 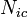 contacts with infectious individuals, with infection probability at ith contact given by
contacts with infectious individuals, with infection probability at ith contact given by 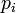 .
.
- disease history includes latent, incubation, and contagious periods of average durations: 1.2, 1.9, and 4.1 days, respectively.
- model implemented in the molecular dynamics SPaSM code, substituting atoms by agents
- basic reproductive number
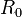 in the range [1.6;2.4] - as parameter of simulations
in the range [1.6;2.4] - as parameter of simulations - initial conditions: 1-10 per 10000 arriving flight passengers randomly infected, only once for the whole simulation
Stroud's, in southern California, USA[8]
- model implemented in EpiSimS platform
References
- ↑ CAUCHEMEZ S, Valleron A J, Boelle P Y, Flahault A, and Ferguson N M, Estimating the impact of school closure on influenza transmission from Sentinel data, Nature, 452 (2008), pp.750-754
- ↑ CAUCHEMEZ S, Carrat F, Viboud C, Valleron A J, Boelle P Y, A Bayesian MCMC approach to study transmission of influenza: application to household longitudinal data, Stat. Med., 23, (2004), p3469
- ↑ FERGUSON N M, Cummings D A T, Fraser C, Cajka J C, Cooley P C, and Burke D S, Strategies for mitigating an influenza pandemic, Nature, 442 (2006), pp. 448-452
- ↑ FERGUSON N M, Cummings D, Cauchemez S, Fraser C, Riley S, Meeyai A, Iamsirithaworn S, and Burke D, Strategies for containing an emerging influenza pandemic in Southeast Asia, Nature, 437 (2005), pp. 209-214
- ↑ FERGUSON N M, Donnelly C, and Anderson R A, Transmission intensity and impact of control policies on the foot and mouth epidemic in Great Britain, Nature, 413 (2001), pp. 542-548
- ↑ DUNHAM J B, An Agent-Based Spatially Explicit Epidemiological Model in MASON Journal of Artificial Societies and Social Simulation,2005, 9(1)3
- ↑ GERMANN T C, Kadau K, Longini I, and Macken C, Mitigation strategies for pandemic influenza in the United States, Proc. Nat. Acad. Sci., 103 (2006), pp.5935-5940
- ↑ STROUD P, Del Valle S, Sydoriak S, Riese J and Mniszewski S (2007). Spatial Dynamics of Pandemic Influenza in a Massive Artificial Society,Journal of Artificial Societies and Social Simulation 10(4)9