Difference between revisions of "Epidemics"

Revision as of 14:56, 5 November 2008

Virtual society	Virus spread	Literature	Version
Polish virtual society epidemics model
Guinea pigs epidemics model
Virus genetic evolution epidemics model

Pandemics history info on the Internet

Past Pandemic Timeline in Nature

H5N1 outbreaks in birds and other animals in Nature

Human cases of avian flu in Nature

Influenza report 2006 - on-line book

Important parameters

Basic reproductive number, 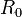$R_0$ - the mean number of secondary cases a typical single infected case will cause in a population with no immunity to the disease in the absence of interventions to control the infection.

Review of epidemics models

Ferguson's, in France^[1]

Quite large amount of data on epidemics in France from Sentinel and Centre National de Reference de la Grippe, region Sud, Laboratoire de Virology.

workplaces not explicitly included
transmission model: probability of the infection of the individual i, 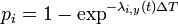$p_i=1-\exp^{-\lambda_{i,y}(t) \Delta T}$ , where 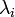$\lambda_i$ is the instantaneous infection risk of the individual i.
transmission rate in a household 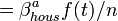$= \beta^{a}_{hous} f(t)/n$ , where a - age (Adult(>=18) or Child), f(t) - relative infectiousness according to time t since infection, n - the size of the household.
transmission rates for: within household infection (A,C), within school, within community (A->A,C->C,A<->C). Hence, the overall risk of infection includes: the household risk, the within school risk, the community risk
time step = 6h
annual variations of influenza infections modeled via: the strength of transmission during the year and the relative contribution of children to transmission during the year (included in 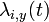$\lambda_{i,y}(t)$ ), where y - year

Ferguson's, in UK and USA^[2]

households, schools, workplaces included in the model
commuting data also included (the average distances traveled from hh to wp); the UK distance distribution more-less like power law, that of USA - surprisingly a bit different
air travel data included
time step = 6h
transmission model: probability of the infection of the individual i, 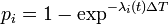$p_i=1-\exp^{-\lambda_i(t) \Delta T}$ , where 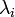$\lambda_i$ is the instantaneous infection risk of the individual i.

Ferguson's, in Thailand^[3]

households, schools, workplaces included in the model
travel data - not enormous, but some, generalized into probabilities of commuting within district
seasonality not included (available data suggested that climate changes do not influence the infectivity rate)

Ferguson's in UK^[4]

Dunham's general model - MASON^[5]

Germann's, in USA^[6]

no seasonal or environmental factors included, no virus evolution effects included
basic geographic unit corresponds to census tract, it is a community of 2000 individuals: age, household size, and employment status distributions match US census data; agents divided into 5 age groups (0-4, 5-18, 9-29, 30-64, 64+ years) or community with no residents, only a workplace of about 100 individuals; in total, about 180000 communities are included; also travel data for the members of community included (in census tracts info);
playgroups or daycare centers, schools, workplaces included; also contacts with people from neighborhood, occasional contacts in churches, supermarket, etc, included
time step = 12h
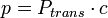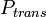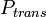transmission model: probability of infection from a single contact, $p = P_{trans}\cdot c$ , where $c$ is the contact probability (dependent on the age of both contacting people), $P_{trans}$ is the probability of transmission; antiviral treatment of the infectious contact person or the vaccination of the given individual diminish the $P_{trans}$ ;

Total probability of the susceptible person to get infected, 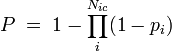$P\;=\;1-\prod_{i}^{N_{ic}}(1-p_{i})$ , where the product goes over all 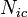$N_{ic}$ contacts with infectious individuals, with infection probability at ith contact given by $p_i$ .

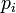disease history includes latent, incubation, and contagious periods of average durations: 1.2, 1.9, and 4.1 days, respectively.
model implemented in the molecular dynamics SPaSM code, substituting atoms by agents
basic reproductive number 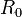$R_0$ in the range [1.6;2.4]

Stroud's, in southern California, USA^[7]

References

↑ CAUCHEMEZ S, Valleron A J, Boelle P Y, Flahault A, and Ferguson N M, Estimating the impact of school closure on influenza transmission from Sentinel data, Nature, 452 (2008), pp.750-754
↑ FERGUSON N M, Cummings D A T, Fraser C, Cajka J C, Cooley P C, and Burke D S, Strategies for mitigating an influenza pandemic, Nature, 442 (2006), pp. 448-452
↑ FERGUSON N M, Cummings D, Cauchemez S, Fraser C, Riley S, Meeyai A, Iamsirithaworn S, and Burke D, Strategies for containing an emerging influenza pandemic in Southeast Asia, Nature, 437 (2005), pp. 209-214
↑ FERGUSON N M, Donnelly C, and Anderson R A, Transmission intensity and impact of control policies on the foot and mouth epidemic in Great Britain, Nature, 413 (2001), pp. 542-548
↑ DUNHAM J B, An Agent-Based Spatially Explicit Epidemiological Model in MASON Journal of Artificial Societies and Social Simulation,2005, 9(1)3
↑ GERMANN T C, Kadau K, Longini I, and Macken C, Mitigation strategies for pandemic influenza in the United States, Proc. Nat. Acad. Sci., 103 (2006), pp.5935-5940
↑ STROUD P, Del Valle S, Sydoriak S, Riese J and Mniszewski S (2007). Spatial Dynamics of Pandemic Influenza in a Massive Artificial Society,Journal of Artificial Societies and Social Simulation 10(4)9

[ferguson2008-1] CAUCHEMEZ S, Valleron A J, Boelle P Y, Flahault A, and Ferguson N M, Estimating the impact of school closure on influenza transmission from Sentinel data, Nature, 452 (2008), pp.750-754

[ferguson2006-2] FERGUSON N M, Cummings D A T, Fraser C, Cajka J C, Cooley P C, and Burke D S, Strategies for mitigating an influenza pandemic, Nature, 442 (2006), pp. 448-452

[ferguson2005-3] FERGUSON N M, Cummings D, Cauchemez S, Fraser C, Riley S, Meeyai A, Iamsirithaworn S, and Burke D, Strategies for containing an emerging influenza pandemic in Southeast Asia, Nature, 437 (2005), pp. 209-214

[ferguson2001-4] FERGUSON N M, Donnelly C, and Anderson R A, Transmission intensity and impact of control policies on the foot and mouth epidemic in Great Britain, Nature, 413 (2001), pp. 542-548

[dunham2005-5] DUNHAM J B, An Agent-Based Spatially Explicit Epidemiological Model in MASON Journal of Artificial Societies and Social Simulation,2005, 9(1)3

[germann2006-6] GERMANN T C, Kadau K, Longini I, and Macken C, Mitigation strategies for pandemic influenza in the United States, Proc. Nat. Acad. Sci., 103 (2006), pp.5935-5940

[stroud2007-7] STROUD P, Del Valle S, Sydoriak S, Riese J and Mniszewski S (2007). Spatial Dynamics of Pandemic Influenza in a Massive Artificial Society,Journal of Artificial Societies and Social Simulation 10(4)9

[1]

[2]

[3]

[4]

[5]

[6]

[7]

@@ Line 15: / Line 15: @@
 [http://www.influenzareport.com/ Influenza report 2006 - on-line book]
+== Important parameters ==
+* [http://en.wikipedia.org/wiki/Basic_reproductive_rate Basic reproductive number, <math>R_0</math>] -  the mean number of secondary cases a typical single infected case will cause in a population with no immunity to the disease in the absence of interventions to control the infection.
 == Review of epidemics models ==

Difference between revisions of "Epidemics"

Revision as of 14:56, 5 November 2008

Contents

Pandemics history info on the Internet

Important parameters