Epidemics:guineapigs:model
Model's assumptions
We have formulated a discrete stochastic model based on the probability of infection. To estimate this probability, we apply a simple generalized linear model (GLM), with 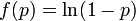 as the link function. This is a standard approach that has been successfully adopted in various related contexts for modeling influenza[1][2]. The model starts from day zero, when all non pre-infected animals are healthy. For each consecutive day, we calculate the probabilities that each individual, among those not yet infected, will be infected on that day, and then we randomly check whether any of the possible infections actually happens.
The infection history is subsequently updated, and the algorithm moves to the next day.
as the link function. This is a standard approach that has been successfully adopted in various related contexts for modeling influenza[1][2]. The model starts from day zero, when all non pre-infected animals are healthy. For each consecutive day, we calculate the probabilities that each individual, among those not yet infected, will be infected on that day, and then we randomly check whether any of the possible infections actually happens.
The infection history is subsequently updated, and the algorithm moves to the next day.
We assume the four following conditions:
1. The probability that the ith individual will be infected on a particular day (provided that it had not been infected previously) is
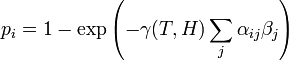
where 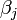 is a measure of virus concentration in the respiratory tract of the jth individual (decimal logarithm of the number of PFU in one ml of its nasal wash). The summation goes over individuals placed on the same and on adjacent shelves. Spatial coefficients
is a measure of virus concentration in the respiratory tract of the jth individual (decimal logarithm of the number of PFU in one ml of its nasal wash). The summation goes over individuals placed on the same and on adjacent shelves. Spatial coefficients 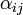 are related to the probabilities that an aerosol drop, shed by the jth animal, will get to the ith guinea pig's cage. The coefficient
are related to the probabilities that an aerosol drop, shed by the jth animal, will get to the ith guinea pig's cage. The coefficient 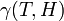 reflects the dependence of the virus transmission rate on the air temperature (T) and relative humidity (H).
reflects the dependence of the virus transmission rate on the air temperature (T) and relative humidity (H).
2. The course of influenza (virus concentration in nasal wash on the days subsequent to infection) depends only on the ambient temperature. Therefore, for each individual that became infected via air during the course of each particular experiment, the concentrations were assigned values reflecting the average case for that temperature. Table 1 shows the mean concentrations measured on particular days after infection, separately for each temperature. Functions comprising two linear pieces appear to be a reasonable guess, as shown in Figure 1.
| Day | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
Concentration, 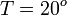
|
1.52 | 4.52 | 5.63 | 6.89 | 6.06 | 3.26 | 1.88 | - | - |
Concentration, 
|
1.91 | 4.40 | 5.72 | 7.02 | 6.01 | 4.54 | 3.52 | 1.77 | - |
| Std. deviation square | 0.40 | 0.59 | 1.26 | 0.32 | 2.38 | 1.44 | 3.18 | 2.34 | - |
The two piecewise linear approximations of the infection course. For  the best fit is the best fit is 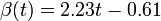 for the growing part and for the growing part and 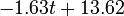 for the falling; for for the falling; for 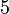 it is it is 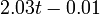 and and  respectively. We assume respectively. We assume  if the amount of virus is undetectable or zero if the amount of virus is undetectable or zero
|
|---|
- Jump up ↑ FERGUSON N M, Cummings D, Cauchemez S, Fraser C, Riley S, Meeyai A, Iamsirithaworn S, and Burke D, Strategies for containing an emerging influenza pandemic in Southeast Asia, Nature, 437 (2005), p209
- Jump up ↑ Stegeman A, Bouma A, Elbers A R W, de Jong M C M, Nodelijk G, de Klerk F, Koch G, van Boven M,Avian Influenza A Virus (H7N7) Epidemic in The Netherlands in 2003: Course of the Epidemic and Effectiveness of Control Measures, J. Inf. Dis. 190, 2004